Go to Home Page

Magic in Billiards 

Armando Rodriguez

President of #include Software Consulting Inc 

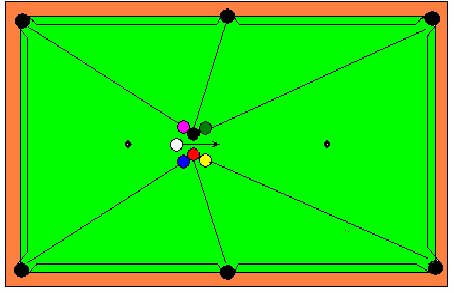
There’s a billiard trick that I love to perform, for which I use a special frame I bought from Jaworski Billiard Co. which holds 6 balls, I place the frame with the balls in the spot where I am instructed to, then I drive the cue ball hard to hit the rather obvious point where I am also instructed to hit and … Shazam! each ball goes into its pocket and the cue ball stays right where it hit! WOW! goes the audience. I never fully enjoyed the success of my performances until I understood how it all worked, now that I think I do, I want to share with you. By the way, do you know much energy is lost in a ball collision? I also found an easy way to measure it.

Defining the Problem

What is knowing how it works? I would be satisfied if I could get the position for the balls using physics and a little geometry.

Figure 1. The “6 in one shot” trick.

Size of the table rail to rail is 88” by 44” , the balls are all identical, 2 ¼” in diameter.

Collision of Two Balls with Equal Mass

Consider Ball 1 that collides at velocity v₀ head on with Ball 2 with equal mass at rest. Energy and linear momentum must be conserved so (I know is common knowledge since Newton, but I need to refer to this equations later on):

½ mv₀²  = ½ mv₁²  + ½ mv₂²                                                                                         (1)       

or

v₀²  = v₁²  + v₂²                                                                                                             (2)

Now momentum conservation:

mv₀  =  mv₁ + mv₂                                                                                                         (3)

or

v₀  = v₁ + v₂                                                                                                                  (4)

then 

(v₁ + v₂)²  = v₁²  + v₂²                                                                                                    (5)

Expanding the square of the sum it gets down to   v₁v₂ = 0. But   v₂ can’t be zero, because then v1 must be greater than 0, meaning it has to go through Ball 2, which is absurd, so :

v₁ = 0                                                                                                                           (6)

v₂  = v₁                                                                                                                         (7)

What if the collision is not head on, but with an angle f? Then, there is a component of the velocity vector on the direction normal to the radial lines. No big deal, you may consider that, in this direction there’s no collision and its velocity stays unaltered. In other words, in an inclined collision… uhhh…better check the  drawing below.

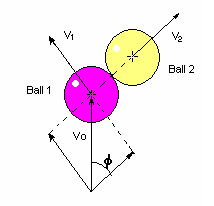
Figure 2. Inclined collision

The ball that hits emerges the collision with a velocity that is at right angle with that of the Ball it hits.

Collision With Multiple Balls in Contact

A system with two balls in contact is not the same as one with two balls glued together. In the first case Ball 1 can push Ball 2, but can not pull, while in the second it can. This makes it a totally different ball game when it comes to collisions. You may look at it like this, if a Ball 0 collides head on with two balls in contact, Ball 0 delivers its energy to Ball 1, Ball 1 to Ball 2 and this one goes away with it. Now consider that Ball 1 is glued to Ball 2, then Ball 2 can not roll away without dragging Ball 1 with it, behaving as an object with twice the mass. So, we may conclude that a collision with multiple balls in contact is actually a multiple collision scenario.

Let us number the balls clockwise like bellow.

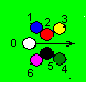
Figure 3. Ball reference numbering

There will be six collisions. If we consider that the cue hits Ball 2 first (it will always hit one of the two first), the six collision will happen in the following order: 0-2; 2-3; 2-1; 0-5; 5-4; 5-6 Hitting Ball 5 first would render the alternative sequence: 0-5; 5-4; 5-6; 0-2; 2-3; 2-1. Of course, in the unlikely case that the cue ball hits 2 and 5 at the same time with such an unearthly precision, collision of one group may interlace with the other, but this is of no consequence. Actually, the behavior of balls 1, 2 and 3 is totally independent of the existence of ball 4, 5 and 6.

Cue Ball Stays Put

The first collisions that must be solved are those of the cue ball with the two center balls. For the cue ball to stay put, its second collision must be a “head on” one. So, if we assume that the cue ball hits Ball 2 first, it must emerge in the head on direction to Ball 5, this can only happen if the centers of the balls 2, 0 and 5 form a right angle.  Two important conclusion can be drawn from this. The center of Ball 2 and Ball 5 must be at Ö2 R from the center line and that if the cue ball doesn’t hit quite exactly between 2 and 5, the rest of the show may work fine, but it won’t stay put, which is a rather cool part of the trick. Actually, it always moves a little, how much? it will be depending on your skill. 

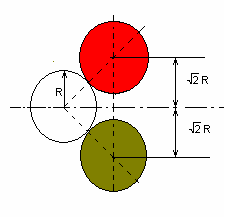
Figure 4.Collision with 2 balls where the cue ball stays put.

Collision with a Three Ball Cluster

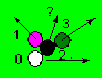
Figure 5. Which direction is the center ball taking after collision?

It is rather obvious in which direction balls 1 and 3 will emerge the collision, but not so with Ball 2. I have heard rather “interesting” answers to this question. The most popular of the wrong ones being: along the middle angle. Another common one, a little more elaborate, is the one that goes: the ball follows the direction of the resulting linear momentum of 1 and 3. But my favorite and, of course, the most flattering, is the one that states that it depends on the speed of the cue ball, thus implying that success depends on the ability of the shooter, that being… me!

The correct answer is quite simple, since the cue ball is coming from the left, the first collision would be 2-3. Ball 2 emerges normal to the 2-3 direction, hitting then Ball 1. Ball 2 will emerge from the 1-2 collision, simply, normal to the 1-2 direction, period! It is not dependent in any way, shape or form to the 2-3 direction. Is this cool, or what?

Figure 6. Ball 2 emerges the collision at right angle with the 2-1 direction

So, we can concentrate on where to place balls 1 and 2, and once we get that right, we can always place Ball 3 so that it points to the right top corner pocket without messing with the solution found for balls 1 and 2.

Eureka! the physics of the problem is solved (for now)…the point of contact between balls 1 and 2, must be such that the direction 1-2 points to the left top corner pocket and the normal from there points to the side top pocket. Recalling that the center of Ball 2 must be Ö2 R from the center line, the rest is a “little geometry”.

A Little Geometry

This “little geometry” can get messy if you start with the wrong foot. To avoid the mess, all you have to do is remember that the locus for point C such that AC is normal to CB is a circumference with diameter AB. So, let A be the top left cornet pocket, B the top side pocket and C the center of Ball 2.

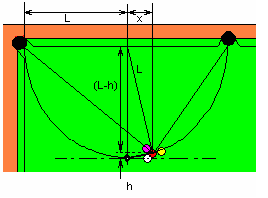
Figure 7. Geometrical auxiliary constructions.

From the drawing, straight Pythagoras yields:

L²=  x² + (L – h)²                                                                                                         (8)

or that:

x = Ö(2Lh – h²)                                                                                                             (9)

Since h = Ö2R                                                                                                               (10)

Evaluating x, you get 8.2”.

It is not an Ideal World

If you try the trick using the above value for x, most of the attempts will fail with the ball hitting the left corner of the side pocket. Once you start trying, you will soon notice that “forcing” the angle or moving the ball to the right gives you a better chance to get the job done, but this makes you wonder, it is clear that Ball 2 is not going normal to the 2-1 direction, what could have gone wrong…? Simply, billiard balls are not as ideally elastic or frictionless as considered in our first approach.

The stuff[a] billiard balls are made of  today was developed to replace ivory. Ivory seems to have been hard enough to minimize energy loss in collisions, but  still soft enough as not to break on impact. This compromised minimum, contrary to Shepard’s opinion[1], is just not small enough for our explanation above to be true. Let’s consider that there is an kinetic energy loss U_L in the head on collision. In principle, this U_L could include, not only heat and sound, but some rotational energy too, if we had to consider frictional forces. But no, there is no need to mess with this, since friction forces are tangential and can’t  affect the velocity component of Ball 2 along the 2-1 radial direction, which would be the one responsible of deviating it from the pocket.

Now (1) or energy conservation goes:

½ mv₀²  = ½ mv₁²  + ½ mv₂² + U_L.                                                                                (10)

Momentum conservation must always holds, so:

v₀  = v₁ + v₂                                                                                                                  (11)

combining:

v₁v₂ = U_L. /m                                                                                                                (12)

Solving for v₁:

v₁ = v₀ /2 (1 – Ö (1-2 U_L./( ½ m v₀ ²)) )                                                              (13)

now for v₂:

v₂ = v₀ /2 (1 + Ö (1-2 U_L./( ½ m v₀ ²)) )                                                                         (14)

Above equations go back to v₁ = 0 and v₂ = v₀ for U_L = 0.  Lets define an energy loss coefficient K_L as:

K_L = U_L./( ½ m v₀ ²)                                                                                                     (15)

Expressions for the v’s in terms of K_L:

v₁ = v₀ /2 (1 – Ö (1-2K_L) )                                                                                            (16)

v₂ = v₀ /2 (1 + Ö (1-2K_L) )                                                                                            (17)

With this new insight, if we consider the inclined collision with an angle f, v₁ will no longer be at a right angle with v_2, since for that, the component of v₁  in the direction of v₂ had to be 0 and that is only true in a perfectly elastic collision. The tangent of angle q that deviates from the normal and thus, the ball from the pocket, is:

tan q = (1 – Ö (1-2K_L) ) / 2 sin f                                                                                  (18)

Notice how the effect is more pronounced as f approaches 0, as a matter of fact, in a head on collision, q is actually 90^o.

Ok…How much is K_L ?

Now comes a pretty cool part of the problem, how can we know K_L? This data should be a spec on a billiard ball set, o even a standard, yet, I’ve never seen spec sheets for billiard balls. I surfed the Internet, but ball manufacturers don’t even mention the issue. So Ok, it could be fun to measure it. I figured that the energy loss of a billiard ball bouncing on tile would be mainly due to absorption by the ball, since tile is much harder and so, deforms a lot less.  On impact, the ball deforms until kinetic energy transforms into elastic energy. Assuming that the linear spring-like model holds for small deformations:

Ue =   ½ S²/s                                                                                                               (19)

Where Ue is elastic energy, S is the strain and s the compliance,  or for S in terms of Ue:

S = Ö(2sUe)                                                                                                                (20)

The combined compliance s for two balls is double that of the ball and tile, since the tile won’t deform at all. Being S proportional to the square root of s, the total deformation in the ball to ball collision, at equal energy, should be Ö2 larger than with the tile. On the other hand, energy loss mechanisms, which are sound and material plasticity, both increase with deformation. It is not too far fetch to claim, at least, proportionality, in which case, the ball to ball K_L should go in the same Ö2 proportion.

Dropping the ball from a height h and measuring how high it bounces back, could render a good value for K. The problem is that it would require a photo sequence to accurately measure the maximum height attained by the bounce, by just looking at it, you’ll probably miss the moment of the maximum and be short in your estimate for h. My “bare eye” estimate for the tile-ball K_L rendered a rough 20%.

Another idea. How about recording the sound from the bouncing of a billiard ball on the tile floor? Great, I had this old sound recording and editing software (Sound Forge 4.5), so I dropped the ball on the tile and recorded the sound of the bounces:

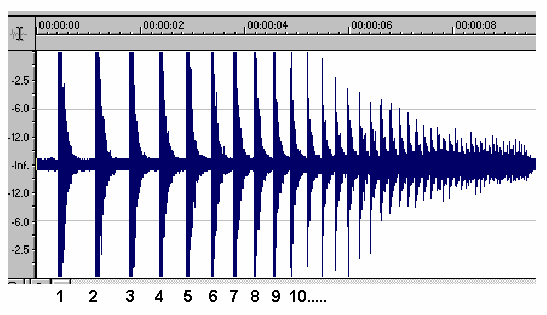
Figure 8. Waveform of the recorded sound. Zooming in allowed millisecond resolution for bounce times

Let t_n be the time between successive bounces n  and n+1, it is related to the height attained by:

h_n = ½ g (t_n/2)²                                                                                                             (21)

But potential energy U_n is equal to gh_n, so:

U_n = g² (t_n)² /8                                                                                                              (22)

And

K_n =( U_n - U_n+1 )/ U_n                                                                                                    (23)

The first ten bounces rendered 7 values for K_n that averaged 0.169  or simply 17%. As expected, it is a little lower than my “bare eye” 20% estimate.

Table 1. Measured values of Kn

The Energy Loss Correction

The angle q, deviation from the right angle, in collision 2-3, would be second order contribution and may safely be neglected, this effect is only noticeable in collision 2-1. 

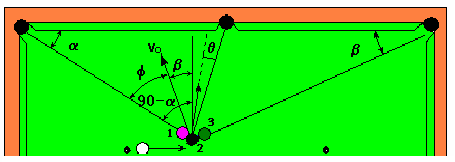
Figure 9: Geometrical construction for calculating the deviation angle q

The inclination angle f for this collision is:

f = 90^o – a - b                                                                                                           (24)

To calculate a and b, we may assume x to be L/2 =11 and (L –h) = 21. yielding:

a = tan ^-1(21/33) = 32.5^o                                                                                              (25)

b = tan ^–1(21/55) = 20.9^o                                                                                             (26)

so,

f = 36.6 ^o                                                                                                                       (27)

Using this value of f and  .17Ö2 for K_n in (18),

tan q = 0.234                                                                                                               (28)

Let the projection of such a correction on the direction of x be Dx

Dx = (L-h) tan q = 4.9”                                                                                                (29)

So x is now 13.1”                                                                                                        (30)

Jaworski Billiards uses still another half an inch. Actually, once in this range, it is not that critical. Now, with this knowledge, you no longer need the Jaworski frame, actually, it is even cooler when you don’t use a special device, it looks more “brainy”. Yet, it would spoil the fun if you had to go for a ruler to perform the trick. Here’s how I do it, I estimate the half way point between the center mark and center of the table (~11”) and place the cue ball there (~12”), now I place balls 2 and 5 conforming a right angle (~12.5”). Once 2 and 5 are in the right spots, the rest of the balls can be placed just by aligning them with the corresponding pockets.

Try it! Hit the cue ball hard and, if you feel you share with me that wonderful feeling of understanding, you may relax and have fun watching your audience in awe!

Bibliography

Books:

Ron Shepard, Amateur Physics for the Amateur Pool Player

Wayland C. Marlow, The Physics of Pocket Billiards

Martin, Ray. The 99 Critical shots in Pool.(1993).New York: Random House Inc.

Mizerak, Steve. Steve Mizerak's complete book of Pool.(1990).Contemporary Books. New York: Steve Mizerak Promotions, Inc.

Web Pages:

http://www.answerbag.com/c_view.php/442

http://www.jimloy.com/billiard/billiard.htm