
The behavior of the FOREX market in the absence of events
also behaves perfectly Brownian. This is to say that FOREX rates behave like an
one dimension random walker. The probability density of finding a random walker
at position x after a time t follows the Gaussian law.
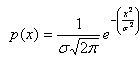 Eq 1
Eq 1
Where s is the standard deviation, that for a random walker is a function of the square root of t and this is what the FOREX rates follow to experimental perfection as shown below for EUR/USD quotes in figure 1.
An analytical expression for the above figure with rates in pips and t in minutes from an initial time t0:
![]() Eq 2
Eq 2
In the average, there are 45 EUR/USD quotes in a minute, so the above expression can be put in terms of the Nth quote after an initial time.
![]() Eq 3
Eq 3
Yet, there is a problem. It is true that the average quotes per minute is around 45, but of those only about 7 are different, meaning that in the average only 1 of every 7 quotes can be considered a step under the random walker model. Even under that consideration, being the average step of 0.6126 pips, a real random walker would wander about 4 times farther than the actual quotes. Is like if there was something “pulling” the quotes towards the average. In other words, say a quote is currently over the average, the chances of it stepping further away are slimmer than the chances of it stepping back. Still another way to put it, say again that the quotes are over the average: a sell is are more likely to win than a buy.
This suggest that when loosing with, say a buy, buying again has a better chance of winning than doing a sell, Conversely, when winning with, say a buy, selling has a better chance of winning again. This, of course, is in the absence of fees and spreads. Winning in the average after these expenses imply that the probability difference has to be big enough and this means time. When a position is held for a long time chances for events hitting safety limits may lower even further the winning chances.
The greatest hurdle for taking advantage of this principle is that at any present moment, no one knows what the average is, because for that, one needs to know the future. So, since there's no way of knowing if quotes are over or under the average, then there's no way of knowing if to buy or to sell. Even if in the long run, it should adjust itself, an investor may go broke before it does.