The Nature of FOREX Market Trends
In the FOREX market, as well as in any other market, the
prices at which you buy or sell a currency with another, slightly changes on
every transaction, a buy will increase this price and a sell will decrease it.
There’s a reason for every transaction; there’s a cause every time buys/sells
supersede sells/buys. If a super-duper computer could be fed with all this
information at the time every transaction happens, then it could predict the
market. But no one has this information and such a computer does not exist
either.
The same problems are common in the human quest for
understanding nature and so, a set of concepts and tools have been developed to
deal with them. This branch of knowledge goes today under the name of statistics.
It treats complex processes in terms of averages and probabilities and this, in
most cases, is all you need to know. An airplane going through the air hits and
gets hit by an enormous number of air molecules, all you need to know is that in
the average, the hits under the wing are likely to be more and stronger than the
hitting on its upper side. Such is the
likelihood, that a flight in any airplane feels perfectly steady. That is the
case of real size airplanes and even model size ones, but what if we kept
reducing the airplane size?
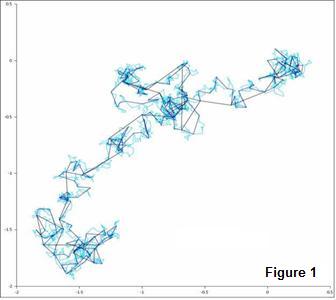
The Brownian motion
 Brownian
motion (named in honor of the botanist
Robert Brown) originally referred to the random motion observed under
microscope of pollen immersed in water. This was puzzling because pollen
particles suspended in perfectly still water had no apparent reason to move all.
Einstein pointed out that this motion was caused by the random bombardment of (heat
excited) water molecules on the pollen. It was just the result of the molecular
nature of matter.
Brownian
motion (named in honor of the botanist
Robert Brown) originally referred to the random motion observed under
microscope of pollen immersed in water. This was puzzling because pollen
particles suspended in perfectly still water had no apparent reason to move all.
Einstein pointed out that this motion was caused by the random bombardment of (heat
excited) water molecules on the pollen. It was just the result of the molecular
nature of matter.
Modern theory calls it a stochastic process and it has
been proven that it can be reduced to the motion a “random walker”. A one
dimensional (1-D) random walker is one that is as likely to take a step forward
as backward, say on the X axis, at any given time. A 2-D random walker does the
same in X or Y (see illustration).
The stock prices change slightly on every transaction, a
buy will increase its price a sell will decrease it. Subject to thousands
of buy
and sell transactions stock prices should show a one-dimensional Brownian
movement. This was the subject of
Louis Bachelier PhD thesis back in 1900, "The theory of speculation.". It
presented a stochastic analysis of the stock and option markets. Currency rates
should behave very much as a pollen particle in water too.
Drift and Trend
Let’s assume now that the pollen particles are floating,
not in still water, but drifting in a flow. Its motion will then be the combined
effect of the drift plus the random one. The drift is the predictable part; the
random, the one that is not. The existence of drift is known or inferred from
macro information affecting all the system, say inclination, wind, some sort of
propeller, etc. The random component can only be treated in terms of averages
and probability.
Back in the FOREX market, drift motion of rates are called
market trends. Some underlying cause is making, say the buys, more likely than
the sells. For instance, consider a
hypothetical case in which a new tax on the manufactures passes US Senate and
the House; speculators figure that this will affect the buying power of the US
dollar and will start selling USD to other currencies, altering their rates
correspondingly. With micro-steps up and down caused by a myriad of shorter term
causes, the GBP/USD will show a longer term up-trend, the USD/JPY a longer term
down trend and so on.
The knowledge of the existence of such a trend does not
mean that an investor selling dollars will automatically make a profit; it just
makes it more likely. A gambling example of a trend is that of counting cards in
a Black Jack game. As the deck of cards thins away, the card counter knows how
many high cards are left in it, so he can estimate his chances of pulling one or
the bank beating him on what he already has. The counter, can't tell what the
next card will be, he just knows the odds or, in other words, he knows the
trend. Yet, that simple knowledge is enough to break the bank.
There is another important estimate, besides the strength
of a trend that an investor has to make. He must figure for how long that trend
is likely to hold. For example, an unemployment report showing a 0.1 point
decrease can hardly overshadow for long the effect of the new tax bill. Any
trend produced by the first event has a foreseeable shorter scope than the
second. So trends have a life span, investments based on trend information must
be strong enough that it can payback within this time span.
Actually what is trend and what is random depends on the
time scale being considered. For events generating trends in the days range,
smaller events causing hourly rates changes are considered random and changes
introduced by any slower longer range trend may be neglected; whereas events
generating trends in the hour range, must consider minutely changes as random
and weekly ones as slow trends to be neglected within that range.
Every rate change is caused by some
event, small events happen all the time, the more transcendental the event; the
fewer they are.
Estimating the Strength of a Trend
The tool for estimating the strength of a trend is the
linear regression. This is a mathematical method that finds the best fitting
line to a data series. This best fitting line is the one in which the sum of the
squared deviations to the data, called residuals, is minimum. The equation of a
line in the xy plane is:
y
= b1
x
+ b0
If the data pairs are (x0,y0), (x1,y1)…
(xi,yi), then the values of
b1 and
b0 minimizing the sum of the
squares of the residuals is:
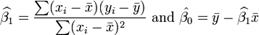
In the above expression the x and y with the bars on top
are the averages of x and y respectively and b1
is the slope of the regression line.
To estimate FOREX rate trends, the y’s should be the rates
and the x’s the timestamps; the slope b1
will indicate the strength of the trend. Still, for the linear regression method
to accurately deliver the strength of a trend, the data must be plentiful and
carefully selected to lie within the saga of the event that caused the trend.
Say an investor receives a piece of news that he/she considers will
generate a trend, first thing to do is verify if the market was indeed sensitive
to the reported event and how sensitive it was. If the event is such that it has
an hourly impact and it happened several hours ago, the linear regression method
applied to the data within these hours will correctly render the strength of
that trend. Had the data for the past day or past week been used, the regression
slope will have nothing to do with the trend being inquired. Also if only the
data of last ten minutes is used, it may not be enough to average out the random
component thus rendering unreliable slope values.
The MHT or Minimum Holding Time
The regression slope relates to the trend strength, since
it is the slope of the line that minimizes the residuals; the line that best
fits the data, but is says nothing about how big these residuals were. The
chances of making a profit on identifying a trend are greatly dependent on the
present market randomness.
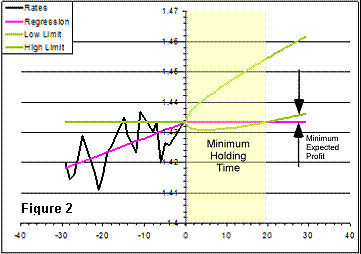 Say
an investor found that the market was sensitive to an event that he/she knew it
happened, but there’s a lot going on besides the effect of that event and the
market is choppy. If this investor opens
a position, he/she must hold that position until the trend has had a chance of
revealing. The nature of the random motion is such that the standard deviation,
or any other interval of confidence, grows with the square root of time, while
the trend makes the rate drift proportional to the time elapsed. This means
that, if the trend holds, and I must be capitalized and underlined: IF THE
TREND HOLDS! Then there’s a time after which it becomes very likely to earn
a profit. This time is the Minimum Holding Time or MHT. Of course there’s a
chance that this investor wins, even if he/she doesn’t wait
Say
an investor found that the market was sensitive to an event that he/she knew it
happened, but there’s a lot going on besides the effect of that event and the
market is choppy. If this investor opens
a position, he/she must hold that position until the trend has had a chance of
revealing. The nature of the random motion is such that the standard deviation,
or any other interval of confidence, grows with the square root of time, while
the trend makes the rate drift proportional to the time elapsed. This means
that, if the trend holds, and I must be capitalized and underlined: IF THE
TREND HOLDS! Then there’s a time after which it becomes very likely to earn
a profit. This time is the Minimum Holding Time or MHT. Of course there’s a
chance that this investor wins, even if he/she doesn’t wait
the MHT, actually in the particular example depicted in
figure 2, the trend is strong and winning chances are always greater. Now, the
two parabolas in green, labeled as low and high limits, plot an interval of
confidence of twice the standard deviation, which equals 95% certainty. In other
words, the interval of confidence is the interval in which you can be 95%
certain to find the rate. The minimum holding time is exactly the moment after
which the chances of winning are above that 95%.
The Walker on the Train Analogy
Abstractions are easier when associating them to graphic
images. Rates and trends are abstractions that can surely make use of one like
the following:
Consider rates to be the position of a random walker on a
track. This random walker, let's call him Johnny, is on a train carrying a
light. Let there be an investor, let's call him Joe, observing this from the
top, on board of, say a balloon or even a static satellite. It is night and the
train is dark, Joe can only see Johnny's light moving back and forth. When Joe
sees the light moving, he cannot tell if it is the train, Johnny or if they both
are moving. At some point Joe gets information from some ground source that the
train might be moving in some direction, say north; Joe starts doing linear
regressions of the positions of Johnny's light in order to figure out the speed
of the invisible train. Joe decides to open a position when Johnny is at
X. At first, Joe may see Johnny going south of X and then back north, but as
time passes, Johnny walks south of X less and less frequent, until this happens
no more. Joe keeps his position open
and watches as his profit grows, but Joe must be careful, for the train could
reverse is motion if new forces develop. So, he must have an estimate of how
long the train will hold its speed in order to maximize his profits.
It is at this point that math can no longer help Joe. How
long will Joe hold his position opened? That will depend on his gut feelings, a
crystal ball or on how much he believes in market inertia. Though the train
analogy was only intended to visualize a mechanism, it may be implicitly suggesting
the existence of market inertia, simply because trains have lots of it. This
market inertia concept has its followers, but since there has been no
statistical proof of its existence, it remains a matter of faith.
One Last Thought About Trends
Trends can be analyzed from a different point of view, one
that doesn’t suggest inertia. Going back to the example of the hypothetical tax
bill that caused a down trend to USD/JPY, what the tax actually did was lowering
the USD buying power and that will finally settle the rate at a new equilibrium
average value. This transition between the initial and final rates created a
trend lasting a limited time interval. The
strength of that trend not only depended on the difference between the initial
and the final rates, but also on the time it took to settle. Highly publicized
news spread fast and so, they can generate strong trends for short period of
times even with small final rate increments. In these cases, media induced panic
is common to cause even some overshooting. Economic events with lower media
impact may produce milder trends even when having greater final increments or
decrements.
A strong trend does not mean that it will last longer than
a mild one; actually it is more likely to be the contrary. An event like the new
tax example will not produce all its effects at once, instead, it will start
triggering a series of child events that may keep the trend going for months.
From this point of view, nothing like market inertia is
suggested; a trend has no conservation tendency, on the contrary, the longer it
remains; the more likely it is that it stops.
 Brownian
motion (named in honor of the botanist
Robert Brown) originally referred to the random motion observed under
microscope of pollen immersed in water. This was puzzling because pollen
particles suspended in perfectly still water had no apparent reason to move all.
Einstein pointed out that this motion was caused by the random bombardment of (heat
excited) water molecules on the pollen. It was just the result of the molecular
nature of matter.
Brownian
motion (named in honor of the botanist
Robert Brown) originally referred to the random motion observed under
microscope of pollen immersed in water. This was puzzling because pollen
particles suspended in perfectly still water had no apparent reason to move all.
Einstein pointed out that this motion was caused by the random bombardment of (heat
excited) water molecules on the pollen. It was just the result of the molecular
nature of matter. Say
an investor found that the market was sensitive to an event that he/she knew it
happened, but there’s a lot going on besides the effect of that event and the
market is choppy.
Say
an investor found that the market was sensitive to an event that he/she knew it
happened, but there’s a lot going on besides the effect of that event and the
market is choppy.