Go to Home Page

Realistic Trajectories for Simulated Air Scenarios

Simulating aircraft motion is currently used for many purposes. In this case we need to simulate an aircraft that must fly through a set of waypoints in a realistic manner. By realistic it is meant that broken line trajectories are not acceptable and that turn radiuses must be considered.

Position Waypoints

Waypoints with Different Altitudes

Climbs and descends further complicate the problem because, in principle, the speed is no longer a “cruise” speed. While in a climb, aircrafts normally slow down and when combined with a turn, the banking angle must be substantially reduced. Even though the increase in distance due to an altitude difference is normally negligible (the first goes in nautical miles and the second in feet), calculation of the flight time may become tricky for nearby waypoints. Also, combined maneuvers raise a lot of options. A climb, for instance, may take less time than a turn, so the climb may be slowed down to match the turn; the climb can be done at the beginning of the turn, at the end, or even completely after the turn during the straight flight. For a simulator to take an optimum choice, the aircraft must be characterized with additional parameters, like power and cargo load which are currently not handled by the simulator.

The policy here will be that the “reality” of simulating waypoints at different altitudes will be transferred to the scenario designer. The simulator will operate as follows:

When a position waypoint is in effect, the m_g[] floating point parameters of waypoints type 3 will have a different interpretation:

Type 3 Way Point

m_g[0]                         Banking angle, in degrees

m_g[1]                         Cruising speed, in knots

m_g[2]                         Max Vertical Rate, in feet per minute.

·         Vertical motion will superimpose to the simulated aircraft motion in the XY plane, which increases the resultant speed.

·         Vertical rate will come into effect right after a waypoint type 3 sets it to a value different than zero.

·         The altitude will start changing at the specified rate until it matches that of the next position way point, at which point the vertical rate will be set back to zero.

·         When a position waypoint is over flown, it will no longer be in effect. When this happens last course will be kept as well as the last altitude.

Trajectories between Waypoints with the Same Altitude

A real aircraft with a real pilot have infinite maneuver choices for flying from one waypoint to the next. For simulation purposes, the trajectory of choice between waypoints of equal altitude will be the one that minimize the flight time, consisting of a turn with maximum banking angle in order to attain a minimum turning radius and then a steady course to the waypoint.

From the above graphic, it is obvious that points within the shaded area are unreachable with the described maneuver, so no waypoints may be specified there.

The problem may be split in two; one part that deals with the calculation of the real flight time between way points and a second part that has to do with the real time trajectory simulation.

Flight Time Calculation

This first part is needed for the planning stage of the simulated flight.  The simulated aircraft, at its current position, reads the position of the waypoint it must fly to. The simulated aircraft will start turning toward this waypoint until it reaches the right course, then it will keep this course until the waypoint is reached. Precisely at this point, a new waypoint must be read, since waypoints are read at their specified time, the flight time must be known at simulation design time.

In other words, the real-time simulator that runs on its DSP must be provided with a sequence of way points, each of which has a time label. Every 100 ms, this real-time simulator will check if it is time for the next waypoint in line to go active. The next waypoint must go active when the present waypoint is reached (or even before but never after). This means that the fly time between waypoints must be known when creating the waypoint sequence, before the simulation starts.

Aircraft Turn Radius

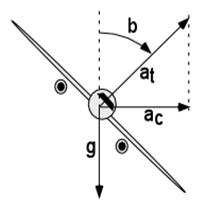The turn radius depends on the cruising speed and the bank angle. This bank angle is limited by the acceleration that the aircraft can withstand. If you tilt a plane in a straight flight, it loses its lift and drops, but it you tilt and pull up, then it turns without dropping. With the right “pull-up”, the inclined lift force is augmented to the point that its vertical component will compensate its weight avoiding the drop in altitude. When a turn is done right, gravity inside the plane is increased while remaining vertical to the floor. You may have experienced this effect while flying when you see that the liquid in you drink stays at level even when the aircraft goes into a turn. So again, in a perfect turn, the bank angle determines the acceleration vector. Let b be the banking angle, a_t the total acceleration and g the acceleration of gravity, then:

cos b = g/ a_t                 eq 1

Then the centripetal acceleration would be.

 a_c = a_t sin b                 eq 2

The turn radius can be then be expressed in terms of the cruise speed Vc and the centripetal acceleration a_t:

R = Vc²/a_c                   eq 3

Manipulating the above expressions we can get to:

R = Vc²/ Ö(a_t² – g²)  or

R = (1.4581759 x 10^-5) Vc²/ Ö(a_t² – 1)            eq 4

That renders R in nautical miles for Vc in knots and a_t in g’s (gravities).  A typical value of a_t for a passenger aircraft is 1.1 that corresponds to banking angle of 24.6 degrees. To the left, there is a table of radiuses and turning rates for this banking angle.

Real Trajectory Length between Position Waypoints

The trajectories within the simulator CPU are calculated using the earth’s ellipsoid model and ECEF Cartesian coordinates, but for accuracies within a second in flight time and latitudes under the Polar Circle, plane geometry should do the job.

Let’s consider an aircraft with a cruising speed Vc and a heading angle b, that, when flying over (0,0) received a waypoint situated at Wx nm to its East and Wy nm to the North (or South as in the example). The total trajectory length P is the sum of the turning arc plus segment b.  

P = Rdb + b                                        eq5

Let L be the distance to the waypoint:

L = Wx + Wy                                      eq6

a is the complement to the initial waypoint bearing:

a = p/2 – (b - atan2(Wx.Wy))            eq7

The cosine law provides an expression for a:

a² = L² + R² + 2RLcos a                     eq8

Since b, a and R make a triangle rectangle:

b² = a² - R² = L² + R² + 2RLcos a                                                      eq9

All we need now is db, but for that we are going to need a few angles to get there…

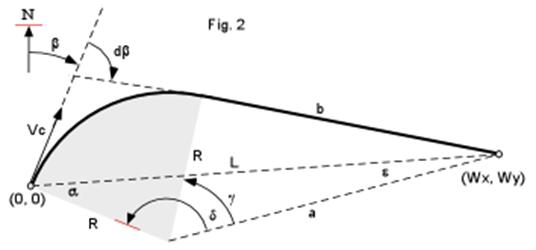
The sine law allows an expression for e:

sin e / R = sin a /a                                                                               eq10

sin g = b/a                                                                                            eq 11

d = p – a – e                                                                                       eq12

Finally:

db = g - d                                                                                           eq13

Flight Time between Position Waypoints

Expression for the flight time Tf is simple:

Tf = P/Vc                                                                                            eq 14

Where P, from eq 5, is the total trajectory length and Vc the cruising speed. However, the above expressions may become tricky to write into a program. This is because the signs and discontinuity of angles may get complicated when attempting to cover the most general case of any angle and any valid waypoint position. A way to simplify things is to reduce every problem to the above. Since any symmetric trajectory renders the same flight time, there’s no great offense in doing this. The heading angle must be reduced to the top quadrants (+/- 90) and the waypoint to the right quadrants. For heading in the bottom quadrants, the scenario must be reflected on X axis. For waypoints on the left quadrants the reflection must be on the Y axis.

Real-Time Trajectory Simulation between Position Waypoints

This part runs in the simulator DSP. Trajectories are calculated in an incremental fashion. Time is divided in dt intervals (one second is actually used), when the timer ticks, position, velocity and acceleration vectors will be incremented in accordance with the motion differential equations. Upon a new waypoint becoming active, the intruder will go into a circular motion with angular speed w until it heads to the waypoint.

w = Vc/R                                                                    eq 15

Where Vc is the cruising speed and R is the turning radius that comes from eq 4. The heading at interval n, H(n), relates to the previous heading as:

H(n) = H(n-1) + dH(n)                                                eq 16

During the turn:

dH =  wdt                                                                   eq 17

At interval n, the aircraft sees the waypoint with bearing angle B(n):

B(n) = H(n-1) - atan2(Wx – X(n-1), Wy – Y(n-1))    eq 18

Where Wx and Wy are the waypoints coordinates; X(n) and Y(n) are the intruder coordinates at interval n. When the bearing angle becomes smaller than wdt, it is time to limit the turn increment dH to the bearing size. So dH(n):

              |  (|B(n)| /B(n)) wdt   for |B(n)| > wdt

dH(n) = |                                                                     eq 19

              |  B(n)                        for |B(n)| < wdt

(|B(n)| /B(n)) is just the sign if B(n), it is 1 if positive and -1 if negative.

Vx(n) and Vy(n) are the projection of the velocity vector at interval n along the X and Y axis respectively, they can be expressed in terms of the bearing heading angle H(n) as:

Vx(n) = Vc*cos(H(n))                                                eq 20

Vy(n) = Vc*sin(H(n))                                                 eq 21

Finally we X(n) and Y(n) can relate to their previous values through the velocity sequence. However, if while turning, the present position is incremented with the non-incremented velocity vector, the next point will lie slightly out of the circle. On the other hand, if the incremented velocity vector is used, the next point this time will lie inside the circle. The error drops more than ten times when the half sum of the two velocity vectors is used for incrementing the position:

X(n) = X(n-1) + ((Vx(n-1)+Vx(n))/2)/3600               eq 22

Y(n) = Y(n-1) + ((Vy(n-1)+Vy(n))/2)/3600               eq 23

Since Vx and Vy are expressed in knots (nm/hour), the one second time increment must be expressed in hours or 1/3600 h. The following is an example of the application of the described algorithm.

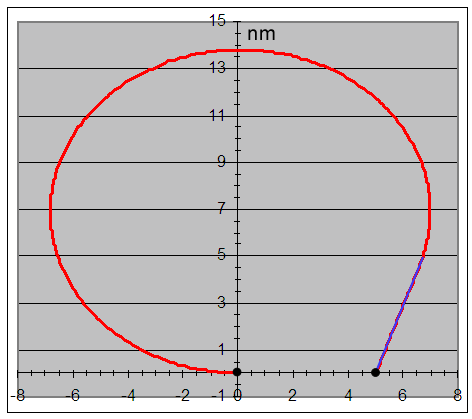
The error in Radius is about 3 feet; had the velocities no been averaged, the error would have been 48 feet.

Velocity Waypoints

A velocity waypoint is one that instructs the simulated aircraft to change course and/or cruising speed without specifying any positional destination. This maneuver may combine centripetal as well as linear acceleration. The resulting trajectory will be, not just an arc, because since the cruising speed may not remain constant, the turning radius may change as it turns, resulting in a segment of an exponential spiral.

In a real flight, the final course may not necessarily be reached at the same time as the final cruising speed. If the cruising speed is attained first, the rest of the turn will be an arc. On the other hand, if the final course is reached first, the trajectory of the maneuver will end in a straight line with linear acceleration only.

A climb may be superimposed without altering to the above described maneuvers even though, in the real world, a climb limits the banking angle and the linear acceleration capabilities of an aircraft. This part of the “reality” is left to the scenario designer.

Flight Time on an Exponential Spiral Trajectory.

Combining equation 1,2,3 and 15 the angular velocity w of the heading in a turn can be expressed in terms of the banking angle b as:

w = (g/Vc) tan(b) = 19.0496765 * tan(b)/Vc  eq 24

(Vc in knots)

Since the aircraft will be accelerating while turning, the cruising velocity is now linear function of time:

Vc = Vc₀ + a_l t                                                            eq 25

Then:

w(t) = g tan(b)/( Vc₀ + a_l t)                              eq 26

In a time interval T, the total heading change DH will be:

óT

DH  = ôw(t) dt                                               eq 27

õ0

Integrating and evaluating at the limits we get DH(T):

DH = (g tan(b)/ a_l) ln(( Vc₀ + a_l T)/ Vc₀)         eq 28

Inverting the equation we get T(DH) or the time necessary for turning the heading in DH:

T = (Vc_0/ a_l)(e^{(|DH| a / ( g tan(b)))}-1)                eq 29

Flight Time for Complying to a Velocity Waypoint

A velocity waypoint specifies a DH and DVc ; let the turning time be T_H (can be calculated with eq 29) and the time to reach the specified new cruise speed be:

Tv = |DVc|./a_l                                                                                      eq 30

If T_V > T_H then the total maneuver time will be T_V, since the turn will be contained into this interval.

The case where T_V < T_H is more complicated, for the first part of the turn is a spiral but the second is an arc. The spiral part will last for T_V seconds and the angle turned will be DH₁, which can be calculated using eq 28:

DH₁ = (g tan(b)/ a_l) ln(( Vc₀ + a_l T_V)/ Vc₀)                             eq 31

The rest of the turn will happen at a constant angular velocity w_f:

w_f = (g tan(b)) /(Vc + DVc)                                                    eq32

T_H = T_V + (DH - DH₁) / w_f                                                     eq 33

Real-Time Trajectory Simulation after a Velocity Waypoint

The sequence for heading angle can be expressed as:

H(n) = H(n-1) + dH(n)                                                            eq 34

Where:

              |  (|B(n)| /B(n)) w(n) dt          for |B(n)| > w(n) dt

dH(n) = |                                                                                 eq 19

              |  B(n)                                    for |B(n)| < w(n) dt

B(n) is the remaining angle to be turned and w(n) the is maximum turning angular velocity.

w(n) = (g tan(b)) /(Vc(n))                                                        eq32

The sequence for cruising speed can be expressed as:

Vc(n) = Vc(n-1)  +  a_l(n)                                                         eq 33

Where if the final cruising speed is Vf:, then:

            | a_l                    for |Vf - Vc(n)| >= a_l

a_l(n) = |                                                                                   eq 34

            | Vf - Vc(n)     for |Vf - Vc(n)| < a_l

The sequence will stop when the calculated flight time has elapsed.